회귀분석 Regression, HR에서의 활용 예시

HR & 빅데이터 2022. 4. 19. 17:33

회귀분석 Regression Analysis

독립변수로 (아직 데이터가 없는) 종속변수를 예측하는 것
- 독립변수는 변수에 영향을 주는 원인이 모델 밖에 있고, 종속변수는 안에 있음
- ex. 대기 오염 정도(독립)가 올라가면 호흡기 질환자 수(종속)가 늘어난다
일반적으로 종속변수가 연속형일 때 (넓게 봐서, 종속변수가 범주형이면 "분류분석")
좁은 의미로는 "선형" 회귀분석만을 말하기도 함
- 독립변수와 종속변수 사이에 "직선적인 형태의 관계가 있다" 는 가정
- 즉, 독립변수의 증가분은 종속변수의 증가분과 (반비례) 관계

회귀 계수 Regression Coefficient

y = [Coefficient] x + [intercept] 독립변수 x가 1 증가할 때마다 종속변수 y는 [Coefficient] 만큼 증가한다.
즉, 독립변수가 x 하나라면, 회귀계수Regression Coefficient 는 직선의 기울기 Slope과 같다
y = [Coefficient1]x1 + [Coefficient2]x2 + .... + [CoefficientN]xN 이라면, coefficient1, 똑같이 출력된다.

절편 Intercept

회귀분석의 사전작업

산점도Scatter Plot와 추세선을 이용해 데이터의 선형적 패턴 확인 (직선의 관계 패턴)
- 극단값이 있을 경우 회귀분석의 결과가 왜곡 될 수 있으므로 주의한다. (어떻게 하지?)
밀도플롯Density Plot이용해 정규분포와 비슷한 형태인지 확인
- 선형회귀분석은 독립변수와 종속변수가 정규분포를 따를 때 잘 작동한다.
- scipy.stats.skew(df['column']) 로 왜도 확인 (-0.11, +0.78정도면 심각하지 않음)

회귀분석 실시

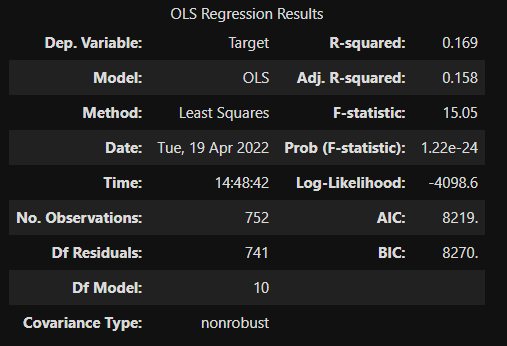
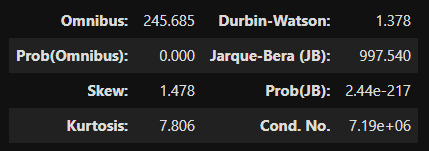
모형적합도

R-squared: 0.169
- R의 제곱
- 모형 적합도(혹은 설명력)
- 단일회귀분석이라고 하면, X독립변수의 분산을 Y종속변수가 [R-squared] %만큼 설명한다.
- 각 사례마다 X독립변수에 차이가 있다.
Adj. R-squared: 0.158
- 독립변수 X가 여러개인 다중회귀분석에서 사용
- 독립변수의 갯수와, 표본의 크기를 고려하여 R-squared를 보정한 값
- 서로 다른 모형을 비교할 때는, 이 지표가 높은 쪽을 선택함.
F-statistic: 15.05, Prob(F-statistic): 1.22e-24
- 회귀모형에 대한 (통계적) 유의미성 검증 결과, 유의미함 (p<0.05)
- 즉, 이 모형은 주어진 표본 뿐 아니라 모집단에서도 의미 있는 모형이라고 할 수 있음.
로그 우도: 종속변수Y가 정규분포라 가정했을 때, 그 우도
- 로그 우도도 R제곱과 마찬가지로 독립변수가 많아지면 증가한다.
- AIC, BIC: 로그우도를 독립변수의 수로 보정한 값 (작을수록 좋은 것)

회귀 계수 (Coefficients)

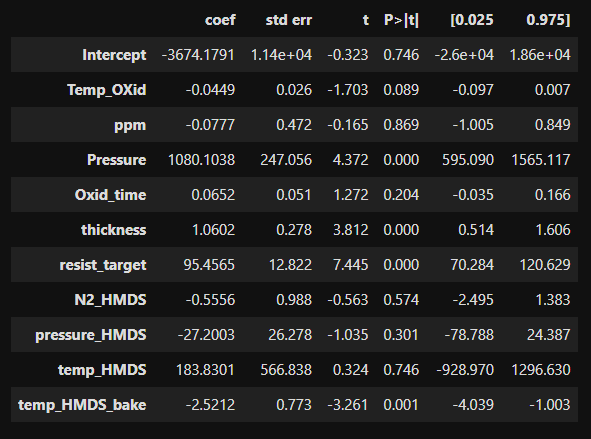
일반적으로 단순회귀분석 결과를 해석 할 때, 결정계수 확인 à 모형의 적합도 확인 à 회귀계수확인 à t값과 t값의 유의확률 확인 순으로 해석을 진행한다.

사실 분석 방법은 큰 의미가 없고... 어떻게 활용 될 것인가가 중요한 듯 하다.

지금 떠오르는 것은 연봉 협상 과정에서의 적절 연봉 산출 정도가 되겠다.

경력 등등 산출 기본 식이 있기는 하겠지만.. 기존 people data를 바탕으로 하는 것이기에 해당 후보자의 우리 회사에서의 Potential을 반영하여 산출할 수 있다는 것이 의미가 있을 듯 하다.