생존분석: 시간에 따른 사건 발생(하지 않을)확률 모델(Survival Analysis for Modeling Singular Events Over Time)
9. Survival Analysis for Modeling Singular Events Over Time
(출처: https://peopleanalytics-regression-book.org/survival.html)
본 포스팅은 위 링크 문서(Handbook of Regression Modeling in People Analytics)를 한국어로 번역한 것입니다.
"Handbook of Regression Modeling in People Analytics: With Examples in R, Python and Julia" was written by Keith McNulty.
*본 내용의 심화된 포스팅은 PA201스터디 페이지(추후 추가 예정) 에 업로드 될 예정입니다.
이전 장에서 우리가 모델링한 결과들은 입력 변수가 측정된 후 특정 시점에 발생했거나 발생하지 않았습니다. 예를 들어, 4장에서 입력 변수는 교육 프로그램의 처음 세 해 동안 측정되었고 결과는 네 번째 해의 끝에 측정되었습니다. 많은 상황에서 우리가 관심 있는 결과는 입력 변수가 측정된 후 언제든지 발생할 수 있고, 개인마다 다른 시간에 발생할 수 있으며, 일단 발생하면 재발하거나 반복될 수 없는 독특한 사건입니다. 의학 연구에서 사망은 연구 기간 동안 언제든지 발생하거나 질병의 발병이 진단될 수 있습니다. 고용 맥락에서 이직 사건은 일 년 내내 다양한 시간에 발생할 수 있습니다.
이를 다루는 명백하고 간단한 방법은 특정 시점을 살펴보기로 합의하고, 그 시점에서 사건이 발생했는지 여부를 측정하는 것일 것입니다. 예를 들어, '세 해 지점에서 몇 명의 직원이 떠났나?'. 이런 접근 방식은 이전 장에서 공부한 표준 일반 회귀 모델과 같은 것을 사용할 수 있게 해줍니다. 하지만 이 접근 방식에는 한계가 있습니다.
첫째, 우리는 연구 기간의 끝에 이르러 사건이 발생했을 가능성에 대한 결론을 추론할 수 있습니다. 우리는 연구 기간 동안 사건의 가능성에 대해 추론할 수 없습니다. 세 해 동안 '언제든지' 특정 유형의 개인에게 이직이 두 배 더 가능하다고 말할 수 있는 것은 단순히 세 해 지점에서 이직이 두 배 더 가능하다고 말하는 것보다 더 강력합니다.
둘째, 우리의 표본 크기는 연구 기간의 끝에서 데이터의 상태에 의해 제한됩니다. 따라서 우리가 만약 개인을 두 해와 여섯 달 후에 추적할 수 없다면, 그 관측은 우리가 세 해 지점에만 초점을 맞춘다면 우리 데이터 세트에서 제거되어야 합니다. 가능한 한 데이터 손실은 통계학자가 피하고자 하는 것이며, 이는 추론의 정확성과 통계적 힘에 영향을 미치며 또한 연구 노력이 낭비되었음을 의미합니다.
생존 분석은 시간과 관련된 이진 비반복 결과의 모델링을 위한 일반적인 용어로, 보통 두 개 이상의 다른 관심 그룹 간의 그 결과의 비교 위험에 대한 이해를 포함합니다. 초보적인 생존 분석에는 다음과 같이 두 가지 일반적인 구성 요소가 있습니다:
- 시간에 따른 다양한 그룹의 미래 결과 위험을 그래픽으로 나타내며, Kaplan-Meier 추정치에 기반한 생존 곡선을 사용합니다. 이것은 일반적으로 특정 입력 변수가 생존 결과와 관련이 있는 것을 처음에 입증하는 효과적인 방법이며, 비통계학자에게 입력 변수의 관련성을 시각적으로 전달하는 매우 효과적인 방법입니다.
- Cox 비례 위험 회귀모델은 연구 기간 동안 결과의 비교 위험에 대한 각 입력 변수의 영향을 추정하고 입력 변수의 통계적 중요성을 입증하기 위한 것입니다.
생존 분석에 대한 보다 깊이 있는 처리를 원하는 사람들은 의학/임상 맥락에서의 사용에 대한 텍스트를 참조해야 하며, 추천되는 출처는 Collett (2015)입니다. 이 장에서는 사람 분석 맥락에서 생존 분석의 전형적인 사용을 설명하기 위해 예제를 통해 설명할 것입니다.
job_retention 데이터 세트는 1년 동안 다양한 고용 분야에서 고용된 약 3,800명의 개인에 대한 연구 결과를 보여줍니다. 연구 시작 시, 개인들은 자신의 직업에 대한 감정을 평가하도록 요청받았습니다. 이 개인들은 그 후 1년 동안 매달 추적되어 같은 직업에 계속 근무하고 있는지 아니면 상당히 다른 직업으로 이직했는지를 확인했습니다. 특정 달에 개인이 성공적으로 추적되지 않은 경우, 그들은 연구 기간의 나머지 기간 동안 더 이상 추적되지 않았습니다.
# if needed, get job_retention data
url <- "http://peopleanalytics-regression-book.org/data/job_retention.csv"
job_retention <- read.csv(url)
head(job_retention)## gender field level sentiment intention left month
## 1 M Public/Government High 3 8 1 1
## 2 F Finance Low 8 4 0 12
## 3 M Education and Training Medium 7 7 1 5
## 4 M Finance Low 8 4 0 12
## 5 M Finance High 7 6 1 1
## 6 F Health Medium 6 10 1 2
이 예제를 통한 설명에서 우리가 관심 있는 특정 분야는 다음과 같습니다:
- gender: 연구 대상 개인의 성별
- field: 연구 시작 시 그들이 일했던 고용 분야
- level: 연구 시작 시 그들의 조직에서의 직위 레벨 - 낮음, 중간, 높음
- sentiment: 연구 시작 시에 1에서 10까지의 척도로 보고된 감정 점수, 1은 매우 부정적인 감정을 나타내고 10은 매우 긍정적인 감정을 나타냄
- left: 마지막 추적 조사 시점에 그 개인이 자신의 직업을 그만두었는지 여부를 나타내는 이진 변수
- month: 마지막 추적 조사의 달
9.1 Tracking and illustrating survival rates over the study period
우리 예제에서, 우리는 '생존'을 '거의 동일한 직업에 남아있는 것'으로 정의합니다. 우리는 시작점을 0월로 간주하며, 우리는 1월부터 12월까지 매달 추적합니다. 주어진 월 i 에 대해, 우리는 생존율 S_i 를 다음과 같이 정의할 수 있습니다.

l_i는 i월에서 이직한 것으로 보고된 숫자이며, n_i는 i 월 이후에 (= n-1 월 후) 거의 동일한 직업에 여전히 있는 숫자입니다. S_0, 즉 초기항은 1로 놓습니다.
R의 survival 패키지는 우리의 job_retention 데이터 세트와 유사한 형식의 데이터에 대한 생존율을 쉽게 구성할 수 있게 해줍니다. survival 객체는 각 시간 기간에서 생존율을 추적하기 위해 Surv() 함수를 사용하여 생성됩니다.
library(survival)
# create survival object with event as 'left' and time as 'month'
retention <- Surv(event = job_retention$left,
time = job_retention$month)
# view unique values of retention
unique(retention)## [1] 1 12+ 5 2 3 6 8 4 8+ 4+ 11 10 9 7+ 5+ 3+ 7 9+ 11+ 12 10+ 6+ 2+ 1+
우리의 생존 객체는 개인이 데이터 세트에 그렇게 기록된 경우에 그들의 직업을 그만둔 달을 기록합니다. 그렇지 않은 경우, 객체는 개인의 기록이 있는 마지막 달을 기록하며, 이것이 사용 가능한 마지막 기록임을 나타내기 위해 '+'로 표시됩니다. (= '+'로 표시되었다면 직업을 그만둔 지 여부는 알지 못하며, 해당 월을 초과한 데이터는 없음을 나타냄.)
survfit() 함수를 사용하면 데이터의 다양한 그룹에 대한 Kaplan-Meier 생존 추정치를 계산하여 비교할 수 있습니다. 우리는 이것을 우리의 일반적인 수식 표기법을 사용하지만 결과로 생존 객체를 사용하여 수행할 수 있습니다. 성별에 따른 생존을 살펴보겠습니다.
# kaplan-meier estimates of survival by gender
kmestimate_gender <- survival::survfit(
formula = Surv(event = left, time = month) ~ gender,
data = job_retention
)
summary(kmestimate_gender)## Call: survfit(formula = Surv(event = left, time = month) ~ gender,
## data = job_retention)
##
## gender=F
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 1 1167 7 0.994 0.00226 0.990 0.998
## 2 1140 24 0.973 0.00477 0.964 0.982
## 3 1102 45 0.933 0.00739 0.919 0.948
## 4 1044 45 0.893 0.00919 0.875 0.911
## 5 987 30 0.866 0.01016 0.846 0.886
## 6 940 51 0.819 0.01154 0.797 0.842
## 7 882 43 0.779 0.01248 0.755 0.804
## 8 830 47 0.735 0.01333 0.709 0.762
## 9 770 40 0.697 0.01394 0.670 0.725
## 10 718 21 0.676 0.01422 0.649 0.705
## 11 687 57 0.620 0.01486 0.592 0.650
## 12 621 17 0.603 0.01501 0.575 0.633
##
## gender=M
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 1 2603 17 0.993 0.00158 0.990 0.997
## 2 2559 66 0.968 0.00347 0.961 0.975
## 3 2473 100 0.929 0.00508 0.919 0.939
## 4 2360 86 0.895 0.00607 0.883 0.907
## 5 2253 56 0.873 0.00660 0.860 0.886
## 6 2171 120 0.824 0.00756 0.810 0.839
## 7 2029 85 0.790 0.00812 0.774 0.806
## 8 1916 114 0.743 0.00875 0.726 0.760
## 9 1782 96 0.703 0.00918 0.685 0.721
## 10 1661 50 0.682 0.00938 0.664 0.700
## 11 1590 101 0.638 0.00972 0.620 0.658
## 12 1460 36 0.623 0.00983 0.604 0.642
우리는 각 그룹의 n.risk, n.event 및 survival 열이 위의 공식에서의 n_i, l_i, s_i 에 해당한다는 것을 볼 수 있으며, 각 생존율의 신뢰 구간이 제공된다는 것을 알 수 있습니다. 이는 주어진 입력 변수가 생존 가능성에 미치는 영향을 설명하고자 할 때 매우 유용할 수 있습니다.
개인의 감정이 생존 가능성에 영향을 미쳤는지 알아보고자 한다고 상상해 봅시다. 우리는 우리 인구를 그들의 감정에 따라 두 그룹 (또는 그 이상)으로 나누고 그들의 생존율을 비교할 수 있습니다.
# create a new field to define high sentiment (>= 7)
job_retention$sentiment_category <- ifelse(
job_retention$sentiment >= 7,
"High",
"Not High"
)
# generate survival rates by sentiment category
kmestimate_sentimentcat <- survival::survfit(
formula = Surv(event = left, time = month) ~ sentiment_category,
data = job_retention
)
summary(kmestimate_sentimentcat)## Call: survfit(formula = Surv(event = left, time = month) ~ sentiment_category,
## data = job_retention)
##
## sentiment_category=High
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 1 3225 15 0.995 0.00120 0.993 0.998
## 2 3167 62 0.976 0.00272 0.971 0.981
## 3 3075 120 0.938 0.00429 0.929 0.946
## 4 2932 102 0.905 0.00522 0.895 0.915
## 5 2802 65 0.884 0.00571 0.873 0.895
## 6 2700 144 0.837 0.00662 0.824 0.850
## 7 2532 110 0.801 0.00718 0.787 0.815
## 8 2389 140 0.754 0.00778 0.739 0.769
## 9 2222 112 0.716 0.00818 0.700 0.732
## 10 2077 56 0.696 0.00835 0.680 0.713
## 11 1994 134 0.650 0.00871 0.633 0.667
## 12 1827 45 0.634 0.00882 0.617 0.651
##
## sentiment_category=Not High
## time n.risk n.event survival std.err lower 95% CI upper 95% CI
## 1 545 9 0.983 0.00546 0.973 0.994
## 2 532 28 0.932 0.01084 0.911 0.953
## 3 500 25 0.885 0.01373 0.859 0.912
## 4 472 29 0.831 0.01618 0.800 0.863
## 5 438 21 0.791 0.01758 0.757 0.826
## 6 411 27 0.739 0.01906 0.703 0.777
## 7 379 18 0.704 0.01987 0.666 0.744
## 8 357 21 0.662 0.02065 0.623 0.704
## 9 330 24 0.614 0.02136 0.574 0.658
## 10 302 15 0.584 0.02171 0.543 0.628
## 11 283 24 0.534 0.02209 0.493 0.579
## 12 254 8 0.517 0.02218 0.476 0.563
우리는 직업에 대한 감정이 높은 사람들에게 생존율이 일관되게 높은 경향이 있음을 볼 수 있습니다. survminer 패키지의 ggsurvplot() 함수는 이를 깔끔하게 시각화할 수 있으며, 그림 9.1에 표시된 것처럼 그룹 간 차이에 대한 추가적인 통계 정보를 제공할 수 있습니다.
library(survminer)
# show survival curves with p-value estimate and confidence intervals
survminer::ggsurvplot(
kmestimate_sentimentcat,
pval = TRUE,
conf.int = TRUE,
palette = c("blue", "red"),
linetype = c("solid", "dashed"),
xlab = "Month",
ylab = "Retention Rate"
)
이는 두 감정 그룹 간의 생존 차이가 통계적으로 유의하며, 연구 기간 동안 감정이 유지에 미치는 영향을 직관적으로 시각화한 것을 확인시켜줍니다.
9.2 Cox proportional hazard regression models
시간 t동안 인구에 대해 모델링하는 생존 결과가 있고, 입력변수들 x_1, x_2, .... , x_p가 그 생존 결과에 어떤 영향을 미치는지에 관심이 있다고 상상해 봅시다. 우리의 생존 결과가 이진변수인 경우, 우리는 어느 시간 t에서의 생존을 이진 로지스틱회귀로 모델링할 수 있습니다. h(t) 를 시간 t에서 생존하지 않은 비율 로 정의하며, 이는 위험함수라고 합니다. 이는 5장에서 우리가 작업했던 내용을 기반으로 합니다.

여기서 h_o(t)는 시간 t에서의 베이스, 또는 절편 위험을 나타내며, b_i는 x_i와 관련된 계수입니다. 이제 우리의 인구에서 두 다른 개인인 A와 B의 위험을 비교한다고 상상해 봅시다. 우리는 개인 A의 위험 곡선 hA(t)와 개인 B의 위험곡선 hB(t) 가 항상 서로 비례하며 절대 교차하지 않는다는 가정을 합니다—이것을 비례 위험 가정이라고 합니다. 이 가정 하에, 우리는 결론을 내릴 수 있습니다.

우리의 최종 방정식에는 t 가 없다는 점을 유의하십시오. 여기서 중요한 관찰은 사람 B의 위험이 사람 A에 비해 일정하고 시간에 독립적이라는 것입니다. 이것은 우리 모델에서 복잡한 요소를 제거할 수 있게 해줍니다. 이것은 입력 변수의 위험에 대한 영향을 시간의 변화를 고려하지 않고도 모델링할 수 있다는 것을 의미하며, 이 모델을 표준 이항 회귀 모델에 대한 해석과 매우 유사하게 만듭니다.
9.2.1 Running a Cox proportional hazard regression model
Cox 비례 위험 모델은 survival 패키지의 coxph() 함수를 사용하여 실행할 수 있으며, 결과는 생존 객체로 설정됩니다. 우리는 성별, 분야, 레벨 및 감정과 같은 입력 변수에 대해 우리의 생존을 모델링해 봅시다.
# run cox model against survival outcome
cox_model <- survival::coxph(
formula = Surv(event = left, time = month) ~ gender +
field + level + sentiment,
data = job_retention
)
summary(cox_model)## Call:
## survival::coxph(formula = Surv(event = left, time = month) ~
## gender + field + level + sentiment, data = job_retention)
##
## n= 3770, number of events= 1354
##
## coef exp(coef) se(coef) z Pr(>|z|)
## genderM -0.04548 0.95553 0.05886 -0.773 0.439647
## fieldFinance 0.22334 1.25025 0.06681 3.343 0.000829 ***
## fieldHealth 0.27830 1.32089 0.12890 2.159 0.030849 *
## fieldLaw 0.10532 1.11107 0.14515 0.726 0.468086
## fieldPublic/Government 0.11499 1.12186 0.08899 1.292 0.196277
## fieldSales/Marketing 0.08776 1.09173 0.10211 0.859 0.390082
## levelLow 0.14813 1.15967 0.09000 1.646 0.099799 .
## levelMedium 0.17666 1.19323 0.10203 1.732 0.083362 .
## sentiment -0.11756 0.88909 0.01397 -8.415 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## exp(coef) exp(-coef) lower .95 upper .95
## genderM 0.9555 1.0465 0.8514 1.0724
## fieldFinance 1.2502 0.7998 1.0968 1.4252
## fieldHealth 1.3209 0.7571 1.0260 1.7005
## fieldLaw 1.1111 0.9000 0.8360 1.4767
## fieldPublic/Government 1.1219 0.8914 0.9423 1.3356
## fieldSales/Marketing 1.0917 0.9160 0.8937 1.3336
## levelLow 1.1597 0.8623 0.9721 1.3834
## levelMedium 1.1932 0.8381 0.9770 1.4574
## sentiment 0.8891 1.1248 0.8651 0.9138
##
## Concordance= 0.578 (se = 0.008 )
## Likelihood ratio test= 89.18 on 9 df, p=2e-15
## Wald test = 94.95 on 9 df, p=<2e-16
## Score (logrank) test = 95.31 on 9 df, p=<2e-16
모델은 다음과 같은 결과를 반환합니다.
- 각 입력 변수에 대한 계수와 그들의 p-값들. 여기서 우리는 재무나 보건 분야에서 일하는 것이 연구 기간 동안 이직할 가능성이 크게 높다는 것과 높은 감정이 이직할 가능성이 크게 낮다는 것을 결론지을 수 있습니다.
- 각 입력 변수와 관련된 상대적 확률 비율. 예를 들어, 감정에서 한 점 추가는 이직 확률을 약 11% 까지 줄입니다. 한 점 감소는 이직 확률을 약 12% 증가시킵니다. 계수에 대한 신뢰 구간도 제공됩니다.
- 계수가 0이라는 귀무 가설에 대한 세 가지 통계적 검정. 이 귀무 가설은 세 가지 검정 모두에 의해 기각되며, 이는 모델이 유의하다는 것을 의미로 해석될 수 있습니다.
중요하게도, 감정이 유지에 중요한 영향을 미친다는 것을 통계적으로 확인함과 동시에, 우리의 Cox 모델은 가능한 매개 변수를 통제할 수 있게 해줍니다. 이제 우리는 동일한 성별, 동일한 분야, 동일한 레벨의 개인들에게도 감정이 유지에 중요한 영향을 미친다고 말할 수 있습니다.
9.2.2 Checking the proportional hazard assumption
이전 섹션에서 언급한 것처럼, Cox 비례 위험 모델이 유효하기 위한 중요한 가정이 있습니다. 이것은 비례 위험 가정이라고 합니다. 항상 그렇듯이, 모델에서 어떤 추론이나 결론을 내리기 전에 이 가정을 확인하는 것이 중요합니다.
이 가정을 검증하는 가장 인기 있는 테스트는 Schoenfeld 잔차라고 알려진 잔차를 사용합니다. 이것은 비례 위험 가정이 유지된다면 시간에 독립적일 것으로 예상됩니다. survival 패키지의 cox.zph() 함수는 Schoenfeld 잔차가 시간에 독립적이라는 귀무 가설에 대한 통계적 테스트를 실행합니다. 이 테스트는 모든 입력 변수와 전체 모델에 대해 수행되며, 유의미한 결과는 비례 위험 가정을 기각할 것입니다.
(ph_check <- survival::cox.zph(cox_model))## chisq df p
## gender 0.726 1 0.39
## field 6.656 5 0.25
## level 2.135 2 0.34
## sentiment 1.828 1 0.18
## GLOBAL 11.156 9 0.27
우리 경우에서, 우리는 비례 위험 가정이 기각되지 않았음을 확인할 수 있습니다. survminer 패키지의 ggcoxzph() 함수는 cox.zph() 검사의 결과를 받아들여 잔차를 시간에 대해 그래프로 나타내어 시각적으로 확인할 수 있게 해줍니다. 이는 그림 9.2에서 볼 수 있습니다.
survminer::ggcoxzph(ph_check,
font.main = 10,
font.x = 10,
font.y = 10)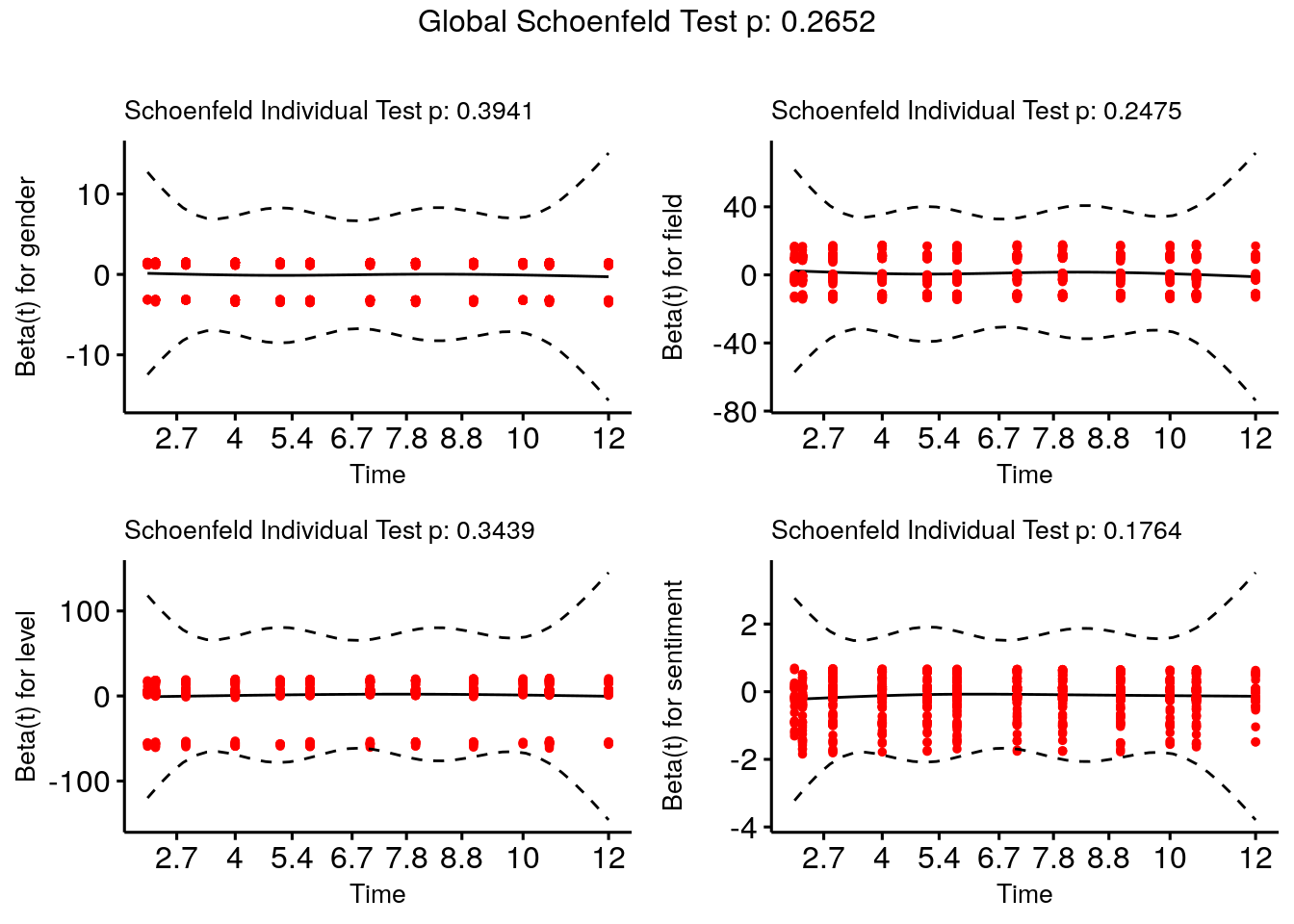
9.3 Frailty models
이전 섹션의 우리 예제에서 우리는 특정 고용 분야가 이직 위험에 중요한 영향을 미치는 것으로 보였습니다. 따라서 다른 고용 분야가 다른 기본 위험 함수를 가질 수 있으며, 우리는 입력 변수가 이직과 중요한 관련이 있는지를 결정하는 데 이를 고려하고자 할 수 있습니다. 이것은 우리가 8.1절에서 살펴본 혼합 모델과 유사합니다.
이 경우에는, 우리는 모델링에서 이를 고려하기 위해 개인의 고용 분야에 따라 기본 위험 함수 hO( t ) 에 랜덤 절편 효과를 적용하고자 합니다. 이러한 유형의 모델은 임상 맥락에서 가져온 취약 모델이라고 하며, 여기서 다른 환자 그룹들은 사망의 다른 취약성(배경 위험)을 가질 수 있습니다.
임상 맥락에서 취약 모델이 실행되는 방식에는 여러 변형이 있습니다(이에 대한 훌륭한 설명은 Collett (2015)를 참조하십시오), 하지만 사람 분석에서 취약 모델의 주요 적용은 데이터의 다른 그룹 간에 발생할 수 있는 위험 사건의 다른 배경 위험을 고려하기 위해 Cox 비례 위험 모델을 적용하는 것입니다. 이것은 공유 취약 모델이라고 합니다. frailtypack R 패키지는 다양한 취약 모델을 상대적으로 쉽게 실행할 수 있게 해줍니다. 우리는 다양한 고용 분야의 다른 배경 이직 위험을 고려하기 위해 우리의 job_retention 데이터에 공유 취약 모델을 실행하는 방법입니다.
library(frailtypack)
(frailty_model <- frailtypack::frailtyPenal(
formula = Surv(event = left, time = month) ~ gender +
level + sentiment + cluster(field),
data = job_retention,
n.knots = 12,
kappa = 10000
))##
## Be patient. The program is computing ...
## The program took 1.24 seconds## Call:
## frailtypack::frailtyPenal(formula = Surv(event = left, time = month) ~
## gender + level + sentiment + cluster(field), data = job_retention,
## n.knots = 12, kappa = 10000)
##
##
## Shared Gamma Frailty model parameter estimates
## using a Penalized Likelihood on the hazard function
##
## coef exp(coef) SE coef (H) SE coef (HIH) z p
## genderM -0.029531 0.970901 0.0591820 0.0591820 -0.498986 6.1779e-01
## levelLow 0.198548 1.219630 0.0917396 0.0917396 2.164255 3.0445e-02
## levelMedium 0.223266 1.250154 0.1035510 0.1035510 2.156101 3.1076e-02
## sentiment -0.108262 0.897392 0.0141325 0.0141325 -7.660518 1.8541e-14
##
## chisq df global p
## level 5.28624 2 0.0711
##
## Frailty parameter, Theta: 48.3209 (SE (H): 25.5895 ) p = 0.029492
##
## penalized marginal log-likelihood = -5510.36
## Convergence criteria:
## parameters = 3.05e-05 likelihood = 4.91e-06 gradient = 1.55e-09
##
## LCV = the approximate likelihood cross-validation criterion
## in the semi parametrical case = 1.46587
##
## n= 3770
## n events= 1354 n groups= 6
## number of iterations: 18
##
## Exact number of knots used: 12
## Value of the smoothing parameter: 10000, DoF: 6.31
우리는 취약성 매개변수가 유의하다는 것을 볼 수 있으며, 이는 배경 이직 위험에서 충분한 차이가 있어 무작위 위험 효과의 적용을 정당화한다는 것을 나타냅니다. 또한, 감정뿐만 아니라 고용 수준이 더 중요해지며, 낮고 중간 수준의 직원들이 높은 수준의 직원들에 비해 이직할 가능성이 더 높다는 것을 볼 수 있습니다.
frailtyPenal() 함수는 데이터의 그룹별 다른 기본 생존을 관찰하는 데 유용한 방법이 될 수도 있습니다. 예를 들어, 감정 카테고리에 기반한 간단한 계층화된 Cox 비례 위험 모델을 구축할 수 있습니다.
stratified_base <- frailtypack::frailtyPenal(
formula = Surv(event = left, time = month) ~
strata(sentiment_category),
data = job_retention,
n.knots = 12,
kappa = rep(10000, 2)
)
이것은 그룹별로 기본 유지율이 어떻게 다른지 관찰하기 위해 그림으로 나타낼 수 있습니다, 예를 들어 그림 9.3과 같이.
plot(stratified_base, type.plot = "Survival",
pos.legend = "topright", Xlab = "Month",
Ylab = "Baseline retention rate",
color = 1)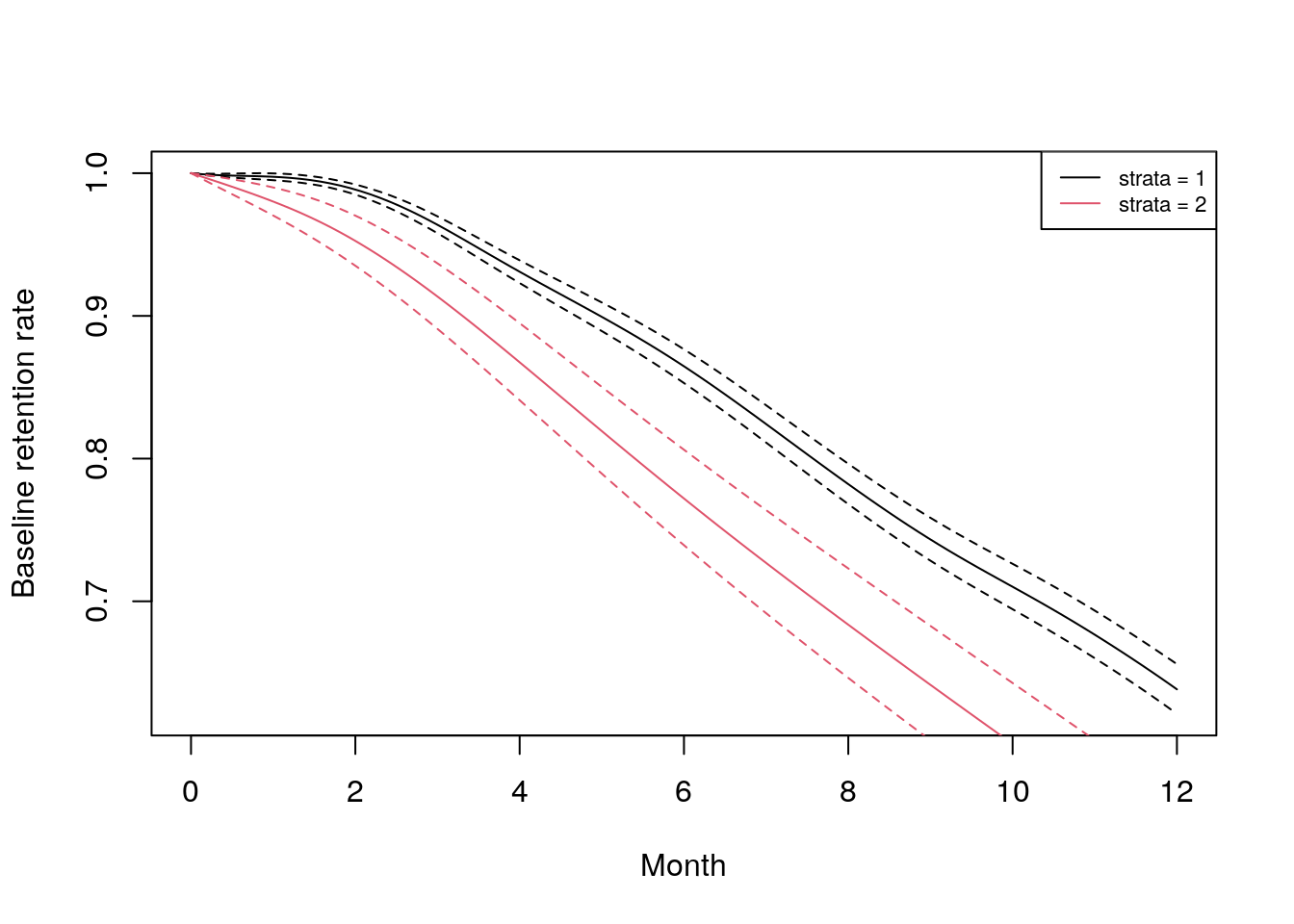
9.4 Learning exercises
9.4.1 Discussion questions
- 결과 사건이 다른 시간에 발생하는 데이터를 분석하는 데 있어 생존 분석이 유용한 도구인 이유를 설명하십시오.
- Kaplan-Meier 생존 추정치를 설명하고 그것이 어떻게 계산되는지 설명하십시오.
- 실제로 생존 곡선을 사용하는 몇 가지 일반적인 용도는 무엇입니까?
- 주어진 변수가 생존에 미치는 영향을 이해하기 위해 생존 추정치를 계산할 뿐만 아니라 Cox 비례 위험 모델을 실행하는 것이 왜 중요합니까?
- Cox 비례 위험 모델에 근거하는 가정을 설명하고 이 가정이 어떻게 확인될 수 있는지 설명하십시오.
- 취약 모델이란 무엇이며, 왜 생존 분석의 맥락에서 유용할 수 있습니까?
9.4.2 Data exercises
이 연습에는 이 장의 예제를 통해 걸어가기 위해 사용된 것과 동일한 job_retention 데이터 세트를 사용하십시오. 이 데이터 세트는 peopleanalyticsdata 패키지를 통해 로드하거나 인터넷에서 다운로드할 수 있습니다. intention 필드는 개인이 다음 12개월 동안 직업을 그만둘 의도를 1에서 10까지의 점수로 나타냅니다. 여기서 1은 매우 낮은 의도를 나타내고 10은 매우 높은 의도를 나타냅니다. 이 응답은 연구 기간 시작 시 기록되었습니다.
- 다음과 같이 의도를 세 가지 카테고리로 생성하십시오: 높음 (7점 이상의 점수), 중간 (4-6점의 점수), 낮음 (3점 이하의 점수)
- 세 가지 카테고리에 대한 Kaplan-Meier 생존 추정치를 계산하고 생존 곡선을 사용하여 이를 시각화하십시오.
- 성별, 분야 및 레벨을 통제하여 의도가 유지에 미치는 영향을 Cox 비례 위험 모델을 사용하여 결정하십시오.
- 귀하의 모델에 대해 비례 위험 가정이 유지되는지 적절한 확인을 수행하십시오.
- 유사한 모델을 실행하지만 이번에는 감정 입력 변수를 포함하십시오.
- 결과를 어떻게 해석하시겠습니까? 고용 분야별 다른 배경 이직 위험을 고려하기 위해 취약 모델을 실행해 보십시오.
