1. 선형대수에서 Norm(노름) 이란?
벡터의 '길이' 또는 '크기'를 측정하는 방법(함수)을 말함.
벡터 공간에 구조를 부여하고, 벡터 간의 거리나 벡터의 크기를 비교하는 데 사용됨.
딥러닝에서 사용되는 노름과 관련하여 이론적인 부분은 더 잘 정리해놓은 다른 글들을 참고하면 더 좋다! (출처: taewan.kim 블로그)
딥러닝을 위한 Norm, 노름
Norm의 정의와 특징을 정리합니다.
taewan.kim
2. Norm(노름) 이 만족시켜야 하는 성질
- 비음수성(Non-negativity): 모든 벡터 에 대해, 노름은 음수가 아니어야 함.
- 결정성(Definiteness): 노름이 0인 경우는 벡터가 영벡터일 때뿐임.
- 동차성(Homogeneity) 또는 스케일 불변성: 스칼라와 벡터에 대해, 이들의 절대값에 비례해야 함.
- 삼각 부등식(Triangle Inequality): 두 벡터 v와 w의 노름의 합은 두 벡터를 합한 벡터의 노름보다 크거나 같아야 함.
"길이나 크기" 라고 했으니까 당연함!
3. 선형대수에서 자주 쓰이는 Norm(노름)
유클리드 노름(Euclidean norm , L2 노름)
가장 일반적인 노름으로, 벡터의 각 요소의 제곱을 합한 후 제곱근을 취한 것.
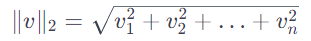
맨해튼 노름(Manhattan norm, 노름)
벡터의 각 요소의 절대값의 합.
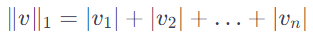
최대 노름(Maximum norm, 노름)
벡터 요소 중 절대값이 가장 큰 요소.

4. 직관적인 적용 예시
ex. 대도시 내 여러 지역들의 사회경제적 지표를 조사하며 다음과 같은 데이터를 수집했을 경우.
- 평균 소득 (단위: 백만원)
- 실업률 (퍼센트)
- 고등교육률 (퍼센트)
- index1. 지역 A: [50, 5, 30] (평균 소득 5천만원, 실업률 5%, 고등교육률 30%)
- index2. 지역 B: [60, 7, 40]
- index3. 지역 C: [55, 6, 35]
이 데이터를 다룬다고 가정할 때, 사회경제적 지위를 나타내는 '크기'를 측정하기 위해 유클리드 노름을 계산할 수 있음.
지역 A의 유클리드 노름(지역A의 사회경제적 지표들의 '크기'):

5. 유클리드노름의 간학문적 적용: 이 둘이 얼마나 차이나는데? 얼마나 가까운데? 에 대한 답을 제공할 수 있음.
언어 패턴 분석: 언어학에서 의미론적 유사성 또는 문맥상 유사성을 분석
텍스트 분석: 문학 작품의 스타일이나 주제를 정량적으로 비교할 때 작가들의 문체나 주제가 얼마나 유사한지를 분석
사회 네트워크 분석: 사회적 관계의 강도나 개인 간의 관계를 분석할 때 노름을 기반으로 사회적 거리를 측정.
정보 검색: 문서나 웹페이지 간의 유사성을 평가할 때, 정보 검색 알고리즘의 핵심 요소로 작용함.
6. HR에서는?
직원 성과 평가: 직원의 성과를 다양한 지표(예를 들어, 판매량, 고객 만족도, 프로젝트 완성 시간 등)로 측정할 때, 각 지표를 벡터의 차원으로 간주 가능. 해당 다차원 성과 벡터의 '길이'를 계산함으로써, 직원의 종합적인 성과 '크기'를 하나의 수치로 표현할 수 있음. 이를 통해 직원들 간의 성과를 비교하고 분석할 수 있음.
직원 역량 분석: 직원의 기술, 경험, 교육 등의 역량을 벡터로 나타낼 수 있음. 각 직원의 역량 벡터의 유클리드 노름을 계산함으로써, 그들의 종합적인 역량을 측정하고 이를 다른 직원이나 필요한 역량 요소와 비교할 수 있음.
직원 만족도 조사: 만족도 조사에서 얻은 다양한 질문에 대한 응답을 벡터로 구성하여, 유클리드 노름을 이용해 각 직원의 만족도 '거리'를 측정할 수 있음. 이를 통해 특정 직원 또는 부서가 회사의 이상적인 만족도 위치에서 얼마나 떨어져 있는지 파악할 수 있음.
직원 교육 및 개발: 직원들의 교육 진행 상황이나 개발 목표 달성 정도를 벡터로 표현하고, 유클리드 노름을 사용하여 각 개인의 진행 정도를 종합적으로 평가할 수 있음.