요즘에 통계학을 다시 듣고 있는데(3번째인데 볼때마다 새로움..) 도전 과제에 봉착했다..
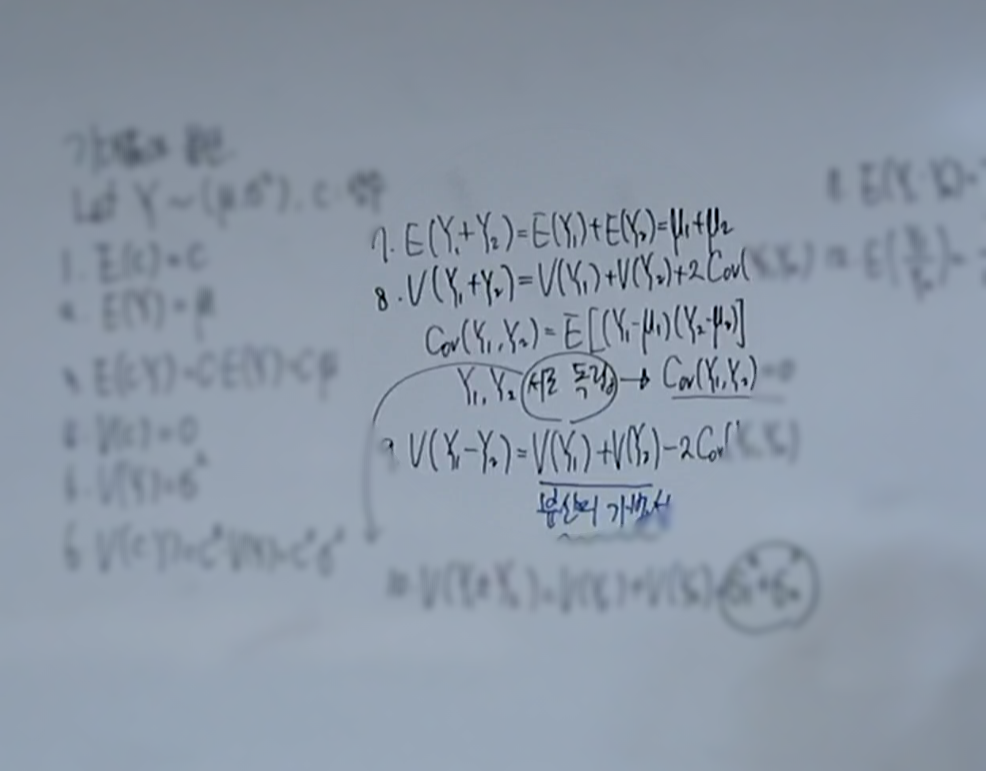
데이터사이언스를 공부하면서 비로소 수학과 통계에 뜻을 두게 된 건, 이 학문이 "실제 우리가 살고 있는 세계를 읽어내는 데 도움이 되는 것" 을 몸소 느껴봤기 때문이었다.
그래서 더 잘하고 싶고, 계속 궁금해졌었는데... 오늘 통계학 듣다가 기댓값과 분산의 성질을 쭉 써주시는데 갑자기 아득해지면서 ㅋㅋㅋㅋ 정신이 산란해지기 시작.
(갠적으로 존경하는 교수님의 강의.. 이지만 외우기 싫은 것과는 별개인 것 같다..)
그래서 구체적으로 기댓값 E(X) 와 분산 V(X)의 개념이 어디에 쓰이는지 좀 적으면서 공부에 대한 셀프 동기부여를 해보고자 한다.
결론부터 말하면 MSE, RMSE, R^2(결정계수) 와 관련이 있다.
- MSE, RMSE = 오차의 기댓값에 가까운 지표
- 결정계수 = 오차의 분산에 가까운 지표이다.
여기까지 보셨으면 사실 포스팅은 끝난거나 다름 없다.
자세한 내용은 아래에 정리해보도록 하겠다!
1. MSE와 RMSE: 오차의 기댓값에 가까움.
MSE (Mean Squared Error) / RMSE(Root Mean Squared Error)
- 잔차(오차)의 제곱을 평균낸 값임. 즉 '오차 제곱을 평균낸 것"
- 엄밀히 말하면 (오차제곱의) 기대값과 비슷한 개념
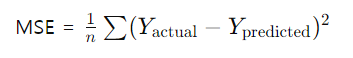
- RMSE는 제곱한 것을 다시 원래 단위로 변환해주는 역할.
- RMSE가 우리가 말하는 '오차의 기대값'에 가깝다고 할 수 있음.
2. R² (결정계수) : 오차의 분산에 가까움.
R²
- 모델이 실제 데이터를 얼마나 잘 설명하는지를 나타내는 지표
- SS_residual 은 잔차 제곱합(Residual Sum of Squres) : 잔차들의 분산 ("모델이 설명하지 못한 변동")
- SS_total : 전체 데이터의 분산 ("전체 데이터의 변동")
- 전체 데이터의 변동variation/분산variance 중에서 얼마나 많은 부분을 설명하고 있는지 나타냄.
- 오차가 얼마나 안정적인지 (모델이 얼마나 안정적인지) 나타낼 수 있음.
- 결정계수가 우리가 말하는 '오차의 분산'에 가깝다고 할 수 있음.
- 왜 "결정계수" 로 번역되는가?
- Coefficient of Determination(결정), Y의 Variation이 X에 의해 얼마나 잘 Determine 되는지 나타내는 계수(Coefficient) 라서 그렇다..
- 선형회귀에서 제일 직관적으로 사용할 수 있고, 약간의 변형을 거치면 비선형회귀 등에서도 사용 가능함.
3. 1,2 는 너무 기본적인 것 같은데.. 그래서 장기적으로 어디에 쓰는데요..?
- 실제 모델링의 성능 개선과 연결
- 위와 연결된 내용이긴 한데, 잔차 개념은 결국 모델의 예측력, 신뢰력을 평가하는 능력에 직결된다. 모델 만들 때 결과를 어느정도 신뢰할 수 있는지, 오차를 어떻게 줄일 수 있는지 파악할 수 있다. 오차(잔차)를 다룰 때 분산개념을 사용해야 하기 때문. 코드 몇줄이면 모델은 어떻게든 만들어진다. "이 모델이 정말 제대로 작동하고 있는가?" 라는 질문에 답할 수 있어야 한다.
- 데이터 변환 및 최적화
- 전처리나 피쳐엔지니어링 할 때 - 스케일링할 때,, 분산이 어떻게 변할지 알면 모델의 학습 속도를 빠르게 하고, 성능을 높일 수 있는 전략을 짤 수 있다. 또, 두 변수의 기댓값이나 분산을 더하거나 빼는 상황은 현실에서 자주 발생한다. 여러개의 변수를 결합할 때 그 효과를 어떻게 다룰지의 문제와 연결.
- 궁극적으로, 더 나은 의사결정 능력
- 예를 들어서, 새로운 캠페인의 성과를 평가한다고 할 때, 기댓값과 분산을 알면 노이즈(noise)와 신호(signal)을 구분할 수 있음. 단순한 우연의 결과인지, 아니면 의미 있는 패턴인지 구분할 수 있다는 이야기.
공부하면 할수록, 특히 기초개념 키워드는 영어의 어원을 같이 보는 게 중요하다는 생각이 든다.
아무튼 동기부여는 조금 되었는데 그래도 다는 못외우겠고.. 나중에 보면 또 알테니.. 몇개만 외우고 넘어가야겠다.
라고 하고 끝에 30초를 더 들었는데, 선형결합으로 이루어진 확률변수의 기댓값과 분산을 다룰 때 필요하다고 딱 말씀을 해 주신다. 뭐 어쨌든 포스팅 하면서 이해 더 잘 했으니 됐다.

기댓값의 선형성 (E(cX) = cE(X))
- 데이터 스케일이 달라졌을 때 기댓값의 변화 (고대로 곱해짐.)
분산의 합과 차
- 7번~11번..

'대학원 일기' 카테고리의 다른 글
| [GCN] Graph Convolution Network에서 샘플링을 안해볼 순 없을까..? (0) | 2024.10.10 |
|---|---|
| [인문학] 고명환 연사 초청 세션 (0) | 2023.11.07 |
| [성균관대 데이터사이언스융합] 대학원 생활 이모저모 (3) | 2023.10.20 |
| [성균관대 데이터사이언스융합] 논자시(논문제출자격시험).. 후기 (15) | 2023.10.12 |
| [석사학위논문] 논문작성 팁 워크숍 요약 (0) | 2023.02.08 |